I just spent a few CPU-months to generate these text files. They catalogue all the “interesting” (from an efficiency and accuracy point of view) polynomial approximations of degree 16 or lower for a couple transcendental functions, over small but useful ranges, in single and double float arithmetic. This claim seems to raise many good questions when people hear it.
What’s wrong with Taylor approximations? Why the need to specify a range?
Why are the results different for single and double floating point arithmetic? Doesn’t rounding each coefficient to the closest float suffice?
Why do I deem only certain approximations to be interesting and others not, and how can there be so few?
In this post, I attempt to provide answers to these interrogations, and sketch how I exploited classic operations research (OR) tools to enter the numerical analysts’ playground.
The final section describe how I’d interpret the catalogue when coding quick and slightly inaccurate polynomial approximations. Such lossy approximations seem to be used a lot in machine learning, game programming and signal processing: for these domains, it makes sense to allow more error than usual, in exchange for faster computations.
The CL code is all up in the repository for rational-simplex, but it’s definitely research-grade. Readers beware.
Minimax approximations
The natural way to approximate functions with polynomials (particularly if one spends time with physicists or engineers) is to use truncated Taylor series. Taylor approximations are usually easy to compute, but only provide good approximations over an infinitesimal range. For example, the degree-1 Taylor approximation for \(\exp\) centered around 0 is \(1 + x\). It’s also obviously suboptimal, if one wishes to minimise the worst-case error: the exponential function is convex, and gradients consistently under-approximate convex functions.
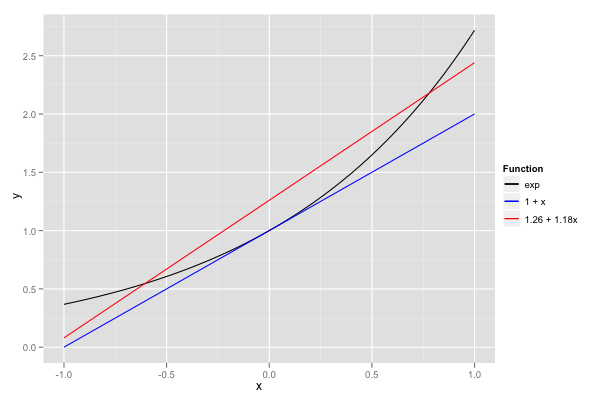
Another affine function, \(1.26 + 1.18x\), intersects \(\exp\) in two points and is overall much closer over \([-1, 1]\). In fact, this latter approximation (roughly) minimises the maximal absolute error over that range: it’s clearly not as good as the Taylor approximation in the vicinity of 0, but it’s also much better in the worst case (all bets are off outside \([-1, 1]\)). That’s why I’m (or anyone’s libm, most likely) not satisfied by Taylor polynomials, and instead wish to compute approximations that minimise the error over a known range; function-specific identities can be exploited to reduce any input to such a range.
Computing minimax polynomials
As far as I know, the typical methods to find polynomial approximation that minimise the maximal error (minimax polynomials) are iterative algorithms in the style of the Remez exchange algorithm. These methods exploit real analysis results to reduce the problem to computing minimax polynomials over very few points (one per coefficient, i.e. one more than the degree): once an approximation is found by solving a linear equation system, error extrema are computed and used as a basis to find the next approximation. Given arbitrary-precision arithmetic and some properties on the approximated function, the method converges. It’s elegant, but depends on high-precision arithmetic.
Instead, I reduce the approximation problem to a sequence of linear optimisation programs. Exchange algorithms solve minimax subproblems over exactly as many points as there are coefficients: the fit can then be solved as a linear equation. I find it simpler to use many more constraints than there are coefficients, and solve the resulting optimisation problem subject to linear inequalities directly, as a linear program.
There are obviously no cycling problems in this cutting planes approach (the set of points grows monotonically), and all the machinery from exchange algorithms can be reused: there is the same need for a good set of initial points and for determining error extrema. The only difference is that points can always be added to the subproblem without having to remove any, and that we can restrict points to correspond to floating values (i.e. values we might actually get as input) without hindering convergence. The last point seems pretty important when looking at high-precision approximations.
For example, let’s approximate the exponential function over \([-1, 1]\) with an affine function. The initial points could simply be the bounds, -1 and 1. The result is the line that passes by \(\exp(-1)\) and \(\exp(1)\), approximately \(1.54 + 1.18x\). The error is pretty bad around 0; solving for the minimax line over three points (-1, 0 and 1) yields a globally optimal solution, approximately \(1.16 + 1.18x\).
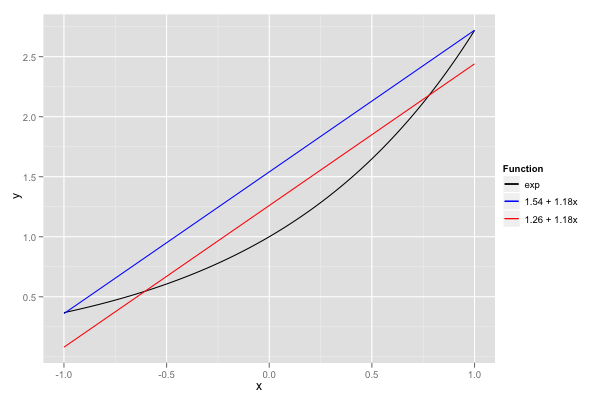
There’s a lot of meat to wrap around this bone. I use a computable reals package in Common Lisp to pull arbitrary-precision rational approximations for arithmetic expressions; using libm directly would approximate an approximation, and likely cause strange results. A variant of Newton’s algorithm (with bisection steps) converges to error extrema (points which can be added to the linear subproblem); arbitrary precision real arithmetic is very useful to ensure convergence down to machine precision here. Each linear subproblem is solved with an exact simplex algorithm in rational arithmetic, and convergence is declared when the value of the error extrema found in the Newton steps correspond to that estimated by the subproblem. Finally, the fact that the input are floating-point values is exploited by ensuring that all the points considered in the linear subproblems correspond exactly to FP values: rather than only rounding a point to the nearest FP value, its two immediately neighbouring (predecessor and successor) FP values were also added to the subproblem. Adding immediate neighbours helps skip iterations in which extrema move only by one ULP.
Initialising the method with a good set of points is essential to obtain reasonable performance. The Chebyshev nodes are known to yield nearly optimal [PDF] initial approximations. The LP-based approach can exploit a large number of starting points, so I went with very many initial Chebyshev nodes (256, for polynomials of degree at most 16), and, again, adjoined three neighbouring FP values for each point. It doesn’t seem useful to me to determine the maximal absolute error very precisely, and I declared convergence when the value predicted by the LP relaxation was off by less than 0.01%. Also key to the performance were tweaks in the polynomial evaluation function to avoid rational arithmetic until the very last step.
Exactly represented coefficients
The previous section gives one reason why there are different tables for single and double float approximations: the ranges of input considered during optimisation differ. There’s another reason that’s more important, particularly for single float coefficients: rounding coefficients can result in catastrophic error blowups.
For example, rounding \(2.5 x\sp{2}\) to the nearest integer coefficient finds either \(2 x\sp{2}\) or \(3 x\sp{2}\). However \(2 x\sp{2} + x\sp{3}\) is also restricted to integer coefficients, but more accurate over \([0, .5]\). Straight coefficient-wise rounding yields an error of \(\frac{1}{2} x\sp{2}\), versus \(\frac{1}{2} x\sp{2} - x\sp{3}\) for the degree-3 approximation. As the following graph shows, the degree-3 approximation is much closer for the range we’re concerned with.
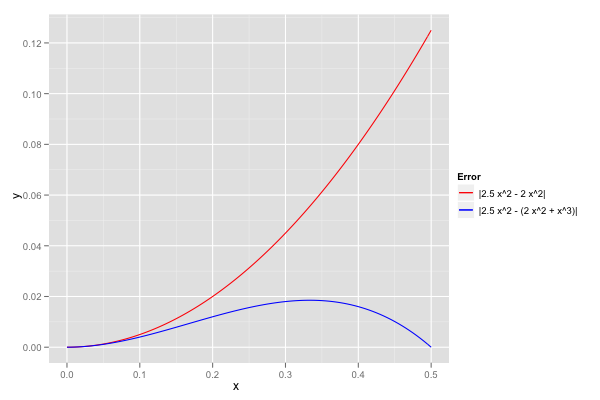
Floating point values are more densely distributed than the integers for the range of values we usually encounter in polynomial approximations, but still discrete, and the same phenomenon crops up, at a smaller scale.
The state of the art for this version of the approximation problem seems to be based on an initial Remez step, followed by a reduction to a CVP.
The cutting planes approach points to a natural solution from the OR world: a branch and cut method. The issue with the cutting planes solution is that, while I only generate points that correspond to FP values, the decision variables (coefficients) are free to take arbitrary rational values.
Branching can be used to split up a decision variable’s range and eliminate from consideration a range of non-FP values. The decision variables’ upper and lower bounds are tightened in a large number of subproblems; solutions gradually converge to all-FP values and their optimality is then proven.
Embedding the cutting planes method in a branch and bound lets us find polynomial approximations with float coefficients that minimise the maximal error over float arguments, with correctly rounded powers. The only remaining simplification is that we assume that the dot product in the polynomial evaluation is error-free. Sadly, removing this simplification results in a horrible discrete optimisation problem with a very bumpy objective function. I’m not sure that any exact approach can solve this in reasonable time. Still, there are ways to evaluate FP polynomials very accurately, and I’m mostly interested in approximations to trade accuracy for speed, so rounding errors may well be negligible compared to approximation errors.
A branch-and-cut method for polynomial approximations
As in all branch and bound methods, a problem is split in subproblems by restricting the range of some coefficient to exclude some infeasible (non-FP) values. For example, in the previous example (in which we’re looking for integer coefficients), the 2.5 coefficient would lead to two subproblems, one in which the degree-2 coefficient is at most 2 \((\lfloor 2.5\rfloor)\), and another in which it’s at least 3 \((\lceil2.5 \rceil)\), excluding all the fractional values between 2 and 3. For floats, we restrict to the closest floats that under- or over- approximate the current value.
However, instead of solving the full continuous relaxation (which is impractical, given the large number of potential argument values), our subproblems are solved with cutting planes. The trick is that cuts (constraints, which correspond to argument values) from any branch can be used everywhere else. Thus, the global point pool is shared between all subproblems, rather than re-generating it from scratch for each subproblem. In practice, this lifting of cutting planes to the root problem seems essential for efficiency; that’s certainly what it took for branch-and-cut MIP solvers to take off.
I generate cuts at the root, but afterwards only when a subproblem yields all-FP values. This choice was made for efficiency reasons. Finding error extrema is relatively slow, but, more importantly, adding cuts really slows down re-optimisation: the state of the simplex algorithm can be preserved between invocations, and warm-starting tends to be extremely efficient when only some variables’ bounds have been modified. However, it’s also necessary to add constraints when an incumbent is all-FP, lest we prematurely declare victory.
There are two really important choices when designing branch and bound algorithms: how the branching variable is chosen, and the order in which subproblems are explored. With polynomial approximations, it seems to make sense to branch on the coefficient corresponding to the lowest degree first: I simply scan the solution and choose the least-degree coefficient that isn’t represented exactly as a float. Nodes are explored in a hybrid depth-first/best-first order: when a subproblem yields children (its objective value is lower than the current best feasible solution, and it isn’t feasible itself), the next node is its child corresponding to the bound closest to the branching variable’s value, otherwise the node with the least predicted value is chosen. The depth-first/closest-first dives quickly converge to decent feasible solutions, while the best-first choice will increase the lower bound, bringing us closer to proving optimality.
A randomised rounding heuristic is also used to provide initial feasible (all-FP) solutions, and the incumbent is considered close enough to optimal when it’s less than 5% off from the best-known lower bound. When the method returns, we have a polynomial approximation with coefficients that are exactly representable as single or double floats (depending on the setting), and which (almost) minimises the approximation error on float arguments.
Interesting approximations
The branch and cut can be used to determine an (nearly-) optimally accurate FP polynomial approximation given a maximum degree. However, the degree isn’t the only tunable to accelerate polynomial evaluation: some coefficients are nicer than others. Multiplying by 0 is obviously very easy (nothing to do), while multiplication by +/-1 is pretty good (no multiplication), and by +/- 2 not too bad either (strength-reduce the multiplication into an addition). It would be possible to consider other integers, but it doesn’t seem to make sense: on current X86, floating point multiplication is only 33-66% slower (more latency) than FP addition, and fiddling with the exponent field means ping-ponging between the FP and integer domains.
There are millions of such approximations with a few “nice” coefficients, even when restricting the search to low degrees (e.g. 10 or lower). However, the vast majority of them will be wildly inaccurate. I decided to only consider approximations that are at least as accurate as the best approximation of degree three lower: e.g. a degree-3 polynomial with nice coefficients is only (potentially) interesting if it’s at least as accurate as a constant. Otherwise, it’s most likely even quicker to just use a lower-degree approximation.
That’s not enough: this filter still leaves thousands of polynomials. Most of the approximations will be dominated by another; what’s the point in looking at a degree-4 polynomial with one coefficient equal to 0 if there’s a degree-3 with one zero that’s just as accurate? The relative importance of the degree, and the number of zeroes, ones and twos will vary depending on the environment and evaluation technique. However, it seems reasonable to assume that zeroes are always at least as quick to work with as ones, and ones as quick as twos. The constant offset ought to be treated distinctly from other coefficients. It’s only added rather than multiplied, so any speed-up is lower, but an offset of 0 is still pretty nice, and, on some architectures, there is special support to load constants like 1 or 2.
This lets me construct a simple but robust performance model: a polynomial is more quickly evaluated than another if it’s of lower or same degree, doesn’t have more non-zero, non-{zero, one} or non-{zero, one, two} multipliers, and if its constant offset is a nicer integer (0 is nicer than +/- 1 is nicer than +/- 2 is nicer than arbitrary floats).
With these five metrics, in addition to accuracy, we have a multi-objective optimisation problem. In some situations, humans may be able to determine a weighting procedure to bring the dimension down to a scalar objective value, but the procedure would be highly domain-specific. Instead, we can use this partial order to report solutions on the Pareto front of accuracy and efficiency: it’s only worth reporting an approximation if there is no approximation that’s better or equal in accuracy and in all the performance metrics. The performance and accuracy characteristics are strongly correlated (decreasing the degree or forcing nice coefficients tends to decrease the accuracy, and a zero coefficient is also zero-or-one, etc.), so it’s not too surprising that there are so few non-dominated solutions.
Enumerating potentially-interesting approximations
The branch and cut can be used to find the most accurate approximation, given an assignment for a few values (e.g. the constant term is 1, or the first degree coefficient 0). I’ll use it as a subproblem solver, in a more exotic branch and bound approach.
We wish to enumerate all the partial assignments that correspond to not-too-horrible solutions, and save those. A normal branch and bound can’t be applied directly, as one of the choices is to leave a given variable free to take any value. However, bounding still works: if a given partial assignment leads to an approximation that’s too inaccurate, the accuracy won’t improve by fixing even more coefficients.
I started with a search in which children were generated by adjoining one fixed value to partial assignments. So, after the root node, there could be one child with the constant term fixed to 0, 1 or 2 (and everything else free), another with the first coefficient fixed to 0, 1 or 2 (everything else left free), etc.
Obviously, this approach leads to a search graph: fixing the constant term to 0 and then the first coefficient to 0, or doing in the reverse order leads to the same partial assignment. A hash table ensures that no partial assignment is explored twice. There’s still a lot of potential for wasted computation: if bounding lets us determine that fixing the constant coefficient to 0 is worthless, we will still generate children with the constant fixed to 0 in other branches!
I borrowed a trick from the SAT solving and constraint programming communities, nogood recording. Modern SAT solvers go far beyond strict branching search: in practice, it seems that good branching orders will lead to quick solutions, while a few bad ones take forever to solve. Solvers thus frequently reset the search tree to a certain extent. However, information is still communicated across search trees via learned clauses. When the search backtracks (an infeasible partial assignment is found), a nogood set of conflicting partial assignments can be computed: no feasible solution will include this nogood assignment.
Some time ago, Vasek Chvatal introduced Resolution Search to port this idea to 0/1 optimisation, and Marius Posta, a friend at CIRRELT and Université de Montréal, extended it to general discrete optimisation [PDF]. The complexity mostly comes from the desire to generate partial assignments that, if they’re bad, will merge well with the current set of learned clauses. This way, the whole set of nogoods (or, rather, an approximation that suffices to guarantee convergence) can be represented and queried efficiently.
There’s no need to be this clever here: each subproblem involves an exact (rational arithmetic) branch and cut. Simply scanning the set of arbitrary nogoods to look for a match significantly accelerates the search. The process is sketched below.
The search is further accelerated by executing multiple branch and cuts and nogood scans in parallel.
The size of the search graph is also reduced by only fixing coefficients to a few values. There’s no point in forcing a coefficient to take the value of 0, 1 or 2 (modulo sign) if it already does. Thus, a coefficient with a value of 0 is left free; otherwise a child extending the partial assignment with 0 is created. Similarly, a child extended with a value of 1 is only generated if the coefficient isn’t already at 0 or 1 (we suppose that multiplication by 0 is at least as efficient as by 1), and similarly for 2. Finally, coefficients between 0 and 1 are only forced to 0 or 1, and those between 1 and 3 to 0, 1 or 2. If a coefficient takes a greater absolute value than 3, fixing it most probably degrades the approximation too strongly, and it’s left free – then again such coefficients only seem to happen on really hard-to-approximate functions like \(\log\) over \([1, 2]\). Also, the last coefficient is never fixed to zero (that would be equivalent to looking at lower-degree approximations, which was done in previous searches). Of course, with negative coefficients, the fixed values are negated as well.
This process generates a large number of potentially interesting polynomial approximations. The non-dominated ones are found with a straight doubly nested loop, with a slight twist: accuracy is computed with machine floating point arithmetic, thus taking rounding into account. The downside is that it’s actually approximated, by sampling fairly many (the FP neighbourhood of 8K Chebyshev nodes) points; preliminary testing indicates that’s good enough for a relative error (on the absolute error estimate) lower than 1e-5. There tends to be a few exactly equivalent polynomials (all the attributes are the same, including accuracy – they only differ by a couple ULP in a few coefficients); in that case, one is chosen arbitrarily. There’s definitely some low-hanging fruit to better capture the performance partial order; the error estimate is an obvious candidate. The hard part was generating all the potentially interesting approximations, though, so one can easily re-run the selection algorithm with tweaked criteria later.
Exploiting the approximation indices
I’m not sure what functions are frequently approximated over what ranges, so I went with the obvious ones: \(\cos\) and \(\sin\) over \([-\pi/2, \pi/2]\), \(\exp\) and arctan over \([-1, 1]\) or \([0, 1]\), \(\log\) over \([1, 2]\), and \(\log 1+x\) and \(\log\sb{2} 1+x\) over \([0, 1]\). This used up a fair amount of CPU time, so I stopped at degree 16.
Each file reports the accuracy and efficient metrics, then the coefficients in floating point and rational form, and a hash of the coefficients to identify the approximation. The summary columns are all aligned, but each line is very long, so the files are best read without line wrapping.
For example, if I were looking for a fairly good approximation of degree 3 for \(\exp\) in single floats, I’d look at exp-degree-lb_error-non_zero-non_one-non_two-constant-error.
The columns report the accuracy and efficiency metrics, in the order used to sort approximations lexicographically:
- the approximation’s degree;
- the floor of the negated base-2 logarithm of the maximum error (roughly bits of absolute accuracy, rounded up);
- the number of non-zero multipliers;
- the number of non-{-1, 0, 1} multipliers;
- whe number of non-{-2, -1, 0, 1, 2} multipliers;
- whether the constant’s absolute value is 0, 1, 2, or other (in which case the value is 3); and
- the maximum error.
After that, separated by pipes, come the coefficients in float form, then in rational form, and the MD5 hash of the coefficients in a float vector (in a contiguous vector, in increasing order of degree, with X86’s little-endian sign-magnitude representation). The hash might also be useful if you’re worried that your favourite implementation isn’t parsing floats right.
There are three polynomials with degree 3, and they all offer approximately the same accuracy (lb_error = 10). I’d choose between the most accurate polynomial
1
| |
or one with a nicer multiplier that doesn’t even double the maximum error
1
| |
On the other hand, if I were looking for an accurate-enough approximation of \(\log 1+x\), I’d open log1px-lb_error-degree-error-non_zero-non_one-non_two-constant.
The columns are in the order used for the lexicographic sort:
- the number of bits of accuracy;
- the approximation’s degree;
- the maximum error;
- the number of non-zero multipliers;
- the number of non-{-1, 0, 1} multipliers;
- the number of non-{-2, -1, 0, 1, 2} multipliers; and
- whether the constant’s absolute value is 0, 1, 2, or other (in which case the value is 3).
An error around 1e-4 would be reasonable for my needs, and
log1px-6AE509 seems interesting: maximum error is around 1.5e-4,
it’s degree 4, the constant offset is 0 and the first multiplier 1.
If I needed a bit more accuracy (7.1e-5), I’d consider log1px-E8200B:
it’s degree 4 as well, and the constant is still 0.
It seems to me optimisation tools like approximation generators are geared toward fire and forget usage. I don’t believe that’s a realistic story: very often, the operator will have a fuzzy range of acceptable parameters, and presenting a small number of solutions with fairly close matches lets them exploit domain-specific insights. In this case, rather than specifying fixed coefficients and degree or accuracy goals, users can scan the indices and decide whether each trade-off is worth it or not. That’s particularly true of the single float approximations, for which the number of possibilities tends to be tiny (e.g. eight non-dominated approximations for \(\sin\)).
